How is Thales' Theorem defined?

From Thales' Theorem, given several parallel lines, the line \(T\) is said to be transversal to the parallel lines if it intersects each of the parallel lines.

In figure 1, the lines \({T_1}\) and \({T_2}\) are transversal to the parallel lines \({L_1}\) and \({L_2}.\)

Thales's theorem (weak version)
If several parallels determine congruent segments (that measure the same) in one of their two transversal lines, they will also determine congruent segments in the other transversals.

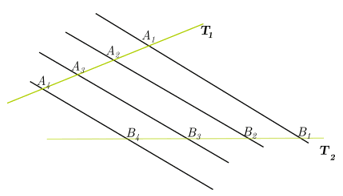
In figure 2, the black lines are parallel and you have to:
\({A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4}.\)
We can ensure the following:
\({B_1}{B_2} = {B_2}{B_3} = {B_3}{B_4}.\)

It is said that the wise Thales of Miletus measured the height of the Cheops pyramid, for this he used shadows and the application of triangle similarity properties. Thales' Theorem is fundamental for the development of the concept of similarity of triangles.

Ratios and properties of proportions

One ratio is the quotient of two numbers, with the divisor other than zero; that is to say:

\(\frac{a}{b}\;{\rm{with\;}}b \ne 0\)

A proportion is the equality of two ratios, that is:

\(\frac{a}{b} = \frac{c}{d} = k,\)

\(k\) is also called the constant of proportionality.

Properties of proportions

If \(\frac{a}{b} = \frac{c}{d} = k\) then for \(m \ne 0:\;\)

\(\frac{{ma}}{{mb}} = \frac{a}{b} = \frac{c}{d} = k\)

\(\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}} = \frac{{a – c}}{{b – d}} = k\)

\(\frac{a}{b} = \frac{c}{d} = \frac{f}{g} = \frac{{a + c + f}}{{b + d + g}} = k\)

\(\frac{{a \pm b}}{b} = \frac{{c \pm d}}{d}\)

examples

\(\frac{9}{{24}} = \frac{{15}}{{40}} = \frac{{9 + 15}}{{24 + 40}} = \frac{{24}} {{64}}\)

\(\frac{9}{{24}} = \frac{{15}}{{40}} = \frac{{15 – 9}}{{40 – 24}} = \frac{6}{{ 16}}\)

\(\frac{{9 + 24}}{{24}} = \frac{{15 + 40}}{{40}}\)\(\frac{{33}}{{24}} = \frac {{55}}{{40}}\)

The pair of segments \(\overline {AB} \) and \(\overline {CD} \) are said to be proportional to the segments \(\overline {EF} \) and \(\overline {GH} \) if the proportion is fulfilled:

\(\frac{{AB}}{{CD}} = \frac{{EF}}{{GH}}\)

Where \(AB\;\) denotes the length of the segment \(\overline {AB} .\)

Thales's theorem

Going back to the definition, several parallels determine proportional corresponding segments in their transversal lines.

In figure 3, the straight lines are parallel and we can ensure:

\(\frac{{{A_1}{A_2}}}{{{A_2}{A_3}}} = \frac{{{B_1}{B_2}}}{{{B_2}{B_3}}}\)\ (\frac{{{A_2}{A_3}}}{{{A_3}{A_4}}} = \frac{{{B_2}{B_3}}}{{{B_3}{B_4}}}\)\( \frac{{{A_2}{A_4}}}{{{A_2}{A_3}}} = \frac{{{B_2}{B_4}}}{{{B_2}{B_3}}}\)\(\frac{{{A_1}{A_2}}}{{{A_3}{A_4}}} = \frac{{{B_1}{B_2}}}{{{B_3}{B_4}}}\)\(\frac{{{A_1}{A_3}}}{{{A_1}{A_2}}} = \frac{{{B_1}{B_3}}}{{{B_1}{B_2}}}\)

Let us note that the first two previous proportions are equivalent to the following proportions:

\(\frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}}\)\ (\frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac{{{A_3}{A_4}}}{{{B_3}{B_4}}}\)Of above we get:

\(\frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac {{{A_3}{A_4}}}{{{B_3}{B_4}}} = \frac{{{A_1}{A_2} + {A_2}{A_3} + {A_3}{A_4}}}{{{B_1}{B_2} + {B_2}{B_3} + {B_3}{B_4}}} = \frac{{{A_1}{A_4}}}{{{B_1}{B_4}}}\)

On many occasions it is better to work with the previous proportions and in this case:

\(\frac{{{A_i}{A_j}}}{{{B_i}{B_j}}} = k\)

Converse of Thales' Theorem

If several lines determine proportional corresponding segments in their transversal lines then the lines are parallel

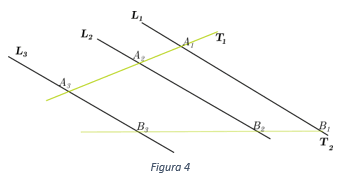
If in figure 4 it is fulfilled

\(\frac{{{A_1}{A_2}}}{{{A_2}{A_3}}} = \frac{{{B_1}{B_2}}}{{{B_2}{B_3}}}\)

Then we can affirm that: \({L_1}\parallel {L_2}\parallel {L_3}.\)

The notation \({L_1}\parallel {L_2}\), read \({L_1}\) is parallel to \({L_2}\).

From the previous proportion we obtain:

\(\frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac {{{A_1}{A_2} + {A_2}{A_3}}}{{{B_1}{B_2} + {B_2}{B_3}}} = \frac{{{A_1}{A_3}}}{{{ B_1}{B_3}}}\)

Division of a segment into several parts of equal length

Through a concrete example we will illustrate how to divide a segment into parts of equal length.

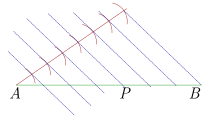
Divide the segment \(\overline {AB} \) into 7 segments of equal length

Initial situation

Draw an auxiliary line that passes through one of the ends of the segment

With the support of a compass, 7 segments of equal length are drawn on the auxiliary line

Draw the line that joins the ends of the last segment drawn and the other end of the segment to be divided

They are drawn parallel to the last line just drawn that pass through the points where the arcs of the circumference intersect with the auxiliary line.

Given a segment \(\overline {AB} \), a point \(P\) of the segment is said to divide the segment \(\overline {AB} \), in the ratio \(\frac{{AP}} {{PB}}.\)

Division of a segment in a given ratio

Given a segment \(\overline {AB} \), and two positive integers \(a, b\); the point \(P\) that divides the segment in the ratio \(\frac{a}{b};\;\) can be found as follows:

1. Divide the segment \(\overline {AB} \) into \(a + b\) segments of equal length.
2. Take \(a\) segments counting from point \(A\).

examples

Division of the segment \(\overline {AB} \) in the ratio \(\frac{a}{b}\)

Reason	Number of parts into which the segment is divided	Location of point \(P\)
\(\frac{{AP}}{{PB}} = \frac{4}{3}\)	\(4 + 3 = 7\)
\(\frac{{AP}}{{PB}} = 6 = \frac{6}{1}\)	\(6 + 1 = 7\)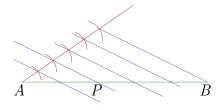
\(\frac{{AP}}{{PB}} = \frac{2}{3}\)	\(2 + 3 = 5\)
\(\frac{{AP}}{{PB}} = \frac{3}{2}\)	\(3 + 2 = 5\)

Applied examples of Thales' Theorem

application 1: Three lots extend from Sol street to Luna street, as shown in figure 5.

The lateral boundaries are segments perpendicular to Luna Street. If the total frontage of the lots on Sol street measures 120 meters, determine the frontage of each lot on said street, if it is also known:

\({A_1}{A_2} = 10{\rm{m}},\;{A_2}{A_3} = 40{\rm{m}},\;{A_3}{A_4} = 20{\rm{ m}},\;{A_4}{A_5} = 30{\rm{m}}.\)

Problem Statement

Since the lines are perpendicular to Luna Street, then they are parallel to each other, by applying Thales' Theorem we can affirm:

\(\frac{{{A_1}{A_2}}}{{{A_2}{A_3}}} = \frac{{{B_1}{B_2}}}{{{B_2}{B_3}}},\; \;\frac{{{A_1}{A_2}}}{{{A_1}{A_4}}} = \frac{{{B_1}{B_2}}}{{{B_1}{B_4}}}\;,\;\;\frac{{{A_1}{A_2}}}{{{A_1}{A_5}} } = \frac{{{B_1}{B_2}}}{{{B_1}{B_5}}}\)Of the above we can conclude:

\(k = \frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_1}{A_4}}}{{{B_1}{B_4}}} = \frac{{{A_1}{A_5}}}{{{B_1}{B_5}}}\;\)

Similarly we can conclude:

\(k = \frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac{{{A_3}{A_4}}}{{{B_3}{B_4}}} = \frac{{{A_4}{A_5}}}{{{B_4}{B_5}}}\)

Solution

To determine the constant of proportionality \(k,\) we will use properties of proportions:

\(k = \frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{{{A_2}{A_3}}}{{{B_2}{B_3}}} = \frac{{{A_3}{A_4}}}{{{B_3}{B_4}}} = \frac{{{A_4}{A_5}}}{{{B_4}{B_5}}} = \frac{{{A_1}{A_2} + {A_2}{A_3} + {A_3}{A_4} + {A_4}{A_5}}}{{{B_1}{B_2} + {B_2}{B_3} + { B_3}{B_4} + {B_4}{B_5}}} = \frac{{{A_1}{A_5}}}{{{B_1}{B_5}}} = \frac{{100}}{{120}} = \frac{5}{6}\)

From the above we get:
\(\frac{{{A_1}{A_2}}}{{{B_1}{B_2}}} = \frac{5}{6}\)\(\frac{{{B_1}{B_2}}}{ {{A_1}{A_2}}} = \frac{6}{5}\)\({B_1}{B_2} = \frac{6}{5}{A_1}{A_2} = \frac{6}{ 5}\left( {10} \right) = 12.\)

Analogously:

\({B_2}{B_3} = \frac{6}{5}{A_2}{A_3} = \frac{6}{5}\left( {40} \right) = 48\)\({B_3} {B_4} = \frac{6}{5}{A_3}{A_4} = \frac{6}{5}\left( {20} \right) = 24\)\({B_4}{B_5} = \frac{6}{5}{A_4}{A_5} = \frac{6 }{5}\left( {30} \right) = 36\)

Answer

Segment	\({B_1}{B_2}\)	\({B_2}{B_3}\)	\({B_3}{B_4}\)	\({B_4}{B_5}\)
Length	12m	48m	24m	36m

application 2: A graphic designer has designed a shelf in the shape of a parallelogram and will place 3 shelves as shown in the Figure 6, points E and F are the midpoints of the sides \(\overline {AD} \) and \(\overline {BC} ,\) respectively. You have to make cuts in the shelves to be able to make the assemblies. In what part of the shelves should the cuts be made?

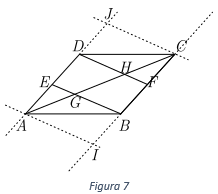
Statement of the problem: Due to the conditions that are given in the problem, the following is fulfilled:

\(ED = EA = CF = BF\)

As auxiliary constructions we will extend the sides \(\overline {CB} \) and \(\overline {DA} \). A line is drawn through point A through \(A\) and parallel to the side \(\overline {EB} \) and through the point \(C\;\) a line is drawn parallel to the side \(\overline {DF} \).

We will use the Converse of Thales' Theorem to show that the segments \(\overline {EB} \) and \(\overline {DF} \) are parallel in order to apply Thales' Theorem.

Solution

By construction the quadrilateral \(EAIB\) is a parallelogram so we have that EA=BI, since they are opposite sides of a parallelogram. Now:

\(\frac{{DE}}{{EA}} = \frac{{BF}}{{BI}} = 1\)

Applying the reciprocal the reciprocal of Thales' Theorem we can conclude:

\(\overline {AI} \parallel \overline {EB} \parallel \overline {DF} \parallel \overline {JC} \)

Taking the segments \(\overline {AI} \parallel \overline {EB} \parallel \overline {DF} \parallel \overline {JC} \) and the segments BC and CI as their transversals; as:

\(FC = BF = BI\)\(CH = HG = GA\)

Taking \(\overline {AD} \parallel \overline {BC} \) and the segments \(\overline {AC} \) and \(\overline {EB} \) as their transversals we will have:

\(\frac{{EG}}{{GB}} = \frac{{AG}}{{GC}} = \frac{{AG}}{{CH + HG}} = \frac{{AG}} {{2\left( {AG} \right)}} = \frac{1}{2}\)

Similarly, it is shown that:

\(\frac{{DH}}{{HF}} = 2\)

Answers

Diagonal cuts \(\overline {AC} \) must be made at points \(G\;\) and \(H\), such that:

\(\frac{{AG}}{{AC}} = \frac{{AH}}{{AC}} = \frac{1}{3}\)

The same is true for the shelves \(\overline {EB} \) and \(\overline {DF} \).