Exponential Function Definition

Inhibition String Theory / by admin / April 02, 2023

Marco Antonio Rodriguez Andrade
Master of Mathematics, Dr. of Science

The exponential function models various natural phenomena and social and economic situations, which is why it is important to identify exponential functions in various contexts.

Let us remember that for a number ${a^1} = a,{a^2} = aa,\;{a^3} = aaa$ is defined, in general we have that for any $n$ number natural:

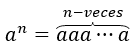
In case $a \ne 0$, we have that: ${a^0} = 1,\;$ in fact, when $a \ne 0,$ it makes sense to do the operation \ (\frac{a}{a} = 1;\) when applying the law of exponents, we have:

$\frac{a}{a} = 1$

${a^{1 – 1}} = 1$

${a^0} = 1.$

When $a = 0$, the previous reasoning does not make sense, therefore, the expression ${0^0},$ lacks a mathematical interpretation.

In the event that $b > 0$ and it is true that ${b^n} = a,$ it is said that $b$ is the nth root of $a$ and is usually denoted as \ (b = {a^{\frac{1}{n}}},\;\) or $b = \sqrt[n]{a}$.

When $a < 0$, there is no real number $b$ such that ${b^2} = a;$ because ${b^2} \ge 0;\;\ ) so expressions of the form \({a^{\frac{m}{n}}}$, will not be considered for $a < 0.$ In the following algebraic expression: ${a^n}$ $a\ ) is called base, and \(n$ is called exponent, ${a^n}$is called the power$\;n$ of $a$ or is also called $a$ to the power $n,\;$se comply with the following laws of the exponents:

instagram story viewer

${a^n}{a^m} = {a^{n + m}}$	$\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}$	${\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}$
$\frac{1}{{{a^n}}} = {a^{ – n}}$	${a^n} = \frac{1}{{{a^{ – n}}}}$	${\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}$
${\left( {ab} \right)^n} = {a^n}{b^n}$	${\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}$	${a^0} = 1$ for each $a \ne 0$

The exponential function is of the form:

$f\left( x \right) = {a^x}$

where $a > 0$ is a constant and the independent variable is the exponent $x$.

To make an analysis of the exponential function, we will consider three cases

Case 1 When the base $a = 1.$

In this case, $a = 1,$ the function $f\left( x \right) = {a^x}$ is a constant function.

Case 2 When the basis $a > 1$

In this case, we have the following:

Value of $x$
$x < 0$	$0 < {a^x} < 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$1 < {a^x} < a$
$x = 1$	${a^x} = 1$
$x > 1$	$a < {a^x}$

The function $f\left( x \right) = {a^x}$ is a strictly increasing function, that is, if ${x_2} > {x_1}$, then:

${a^{{x_2}}} > a_{}^{{x_2}}$

$f\left( {{x_2}} \right) > f\left( {{x_1}} \right)$

When a phenomenon is modeled with an exponential function, with $a > 1$, we say that it presents exponential growth.

Case 2 When the basis $a < 1$.

Value of $x$
$x < 0$	${a^x} > 1$
$x = 0$	${a^0} = 1$
$0 < x < 1$	$0 < {a^x} < 1$
$x = 0$	${a^x} = 1$
$x > 1$	$0 < {a^x} < a < 1$

When $a < 1$, the function $f\left( x \right) = {a^x}$ is a strictly decreasing function, that is, if \({x_2} > {x_1}\ ), so:

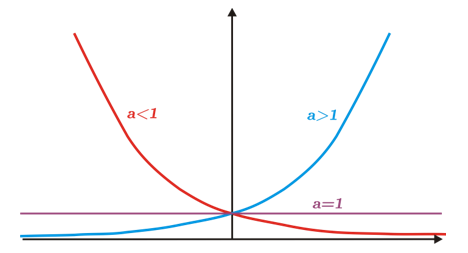
${a^{{x_2}}} < a_{}^{{x_1}}$ $f\left( {{x_2}} \right) < f\left( {{x_1}} \right) $ When a phenomenon is models with an exponential function, with $a < 1$, we say that it presents a decay or decrease exponential. The following graph illustrates the behavior of ${a^x}$, in its three different cases.

Applications of the exponential function

Example 1 Population Growth

We will denote with ${P_0}$ the initial population and with $r \ge 0$ the population growth rate, if the population rate remains constant over time; the function

$P\left( t \right) = {P_0}{\left( {1 + r} \right)^t};$

Find the population at time t.

Practical example 1

The population of Mexico, in the year 2021 is 126 million and presented an annual growth of 1.1%, If this growth is maintained, what population will there be in Mexico in the year 2031, in the year 2021?

Solution

In this case ${P_o} = 126$ and $r = \frac{{1.1}}{{100}} = 0.011$, so you should use:

$P\left( t \right) = {P_0}{\left( {1 + .0011} \right)^t}$

The following table shows the results

Year	elapsed time ($t$)	Calculation	Population (Millions)
2021	0	$P\left( t \right) = 126{\left( {1.0011} \right)^0}$	126
2031	10	$P\left( t \right) = 126{\left( {1.0011} \right)^{10}}$	140.57
2051	30	$P\left( t \right) = 126{\left( {1.0011} \right)^{30}}$	174.95

Example 2 Calculation of compound interest

Banks offer an annual interest rate, but the real rate depends on how many months you invest it; For example, if you are offered an annual interest rate of r%, the real monthly rate is $\frac{r}{{12}}$%, the bimonthly rate is $\frac{r}{6}$%, quarterly is $\frac{r}{4}$%, quarterly is $\frac{r}{3}$%, and the semester is $\frac{r}{2}$%.

Practical example 2

Suppose you invest 10,000 in a bank and they offer you the following annual interest rates:

Fixed term deposits	Annual rate	periods in a year	actual rate	Accumulated money in $k$ months
two months	0.55%	6	$\frac{{0.55\% }}{6} = 0.091667{\rm{\% }}$	$10000{\left( {1 + 0.00091667} \right)^{\frac{k}{2}}}$
three months	1.87%	4	$\frac{{1.87\% }}{4} = 0.4675{\rm{\% }}$	$10000{\left( {1 + 0.00461667} \right)^{\frac{k}{3}}}$
six months	1.56%	2	$\frac{{1.56\% }}{4} = 0.78{\rm{\% }}$	$10000{\left( {1 + 0.0078} \right)^{\frac{k}{6}}}$

The number $e$, Euler's constant and continuous interest.

Now suppose we have an initial capital $C$ and we invest it at a fixed rate $r > 0$, and we divide the year into $n$ periods; the capital accumulated in a year is equal to:

$A = \;C{\left( {1 + \frac{r}{n}} \right)^n}$

To analyze how the accumulated capital behaves when $n$, grows, we will rewrite the accumulated capital, in one year:

$A = \;C{\left( {1 + \frac{r}{n}} \right)^n}$$A = \;C{\left( {1 + \frac{1} {{\frac{n}{r}}}} \right)^{\left( {\frac{n}{r}} \right) r}},$

doing $m = \frac{n}{r}$, we obtain:

$A = C{\left( {1 + \frac{1}{m}} \right)^{mr}}$$A = C{\left( {{{\left( {1 + \ frac{1}{m}} \right)}^m}} \right)^r}.$

As $n$ grows, so does $m = \frac{n}{r}.$

As $m = \frac{n}{r},$ grows the expression ${\left( {1 + \frac{1}{m}} \right)^m}$approaches what is called the Euler constant or number:

$e \approx 2.718281828 \ldots .$

Euler's constant does not have a finite or periodic decimal expression.

We have the following approximations

$C{\left( {{{\left( {1 + \frac{1}{m}} \right)}^m}} \right)^r} \approx C{e^r},$ $C{\left( {1 + \frac{r}{n}} \right)^{ns}} \approx C{e^{rs}}.$

To the expression:

$A = \;C{e^r},$

We can interpret it in two ways:

1.- As the maximum amount that we can accumulate in a year when we invest capital $C,\;$ at an annual rate $r.$

2.- As the amount that we would accumulate, in a year, if our capital were continuously reinvested at an annual rate $r.$

$T\left( s \right) = \;C{e^{rs}},$

is the amount accumulated if $s$ years are invested with continuous interest.

Concrete example 3

Now we will return to a part of concrete example 2, where the annual rate is 0.55% in bimonthly installments. Calculate the capital that accumulates if the initial capital is 10,000 and reinvests half a year, two years, 28 months.

$10{\left( {1.00091667} \right)^{\frac{6}{2}}} = 10.{\rm{\;}}027525$

as the table below shows, the value of $m = \frac{n}{r},$ is not “small” and the table above indicates that ${\left( {1 + \frac{1}{ m}} \right)^m}$ is close to Euler's constant.

Time	Number of periods ($k$)	Accumulated capital, in thousands, reinvested every two months
Half-year	3	$10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525$
Two years	12	$10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557$
38 months	19	$10{\left( {1.00091667} \right)^{19}} = 10.\;175612$

Time	Time of years ($s$)	Accumulated capital, in thousands, invest with continuous interest
Half-year	$s = \frac{1}{2}$	$10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538$
Two years	$s = 2$	$10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607$
38 months	$s = \frac{{19}}{6}$	$10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692$

Example 2 Depreciation

Practical example 1

A computer depreciates 30% each year, if a computer cost $20,000 pesos, determine the price of the computer for $t = 1,12,\;14,\;38$ months.

In this case, one has:

$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – 0.30} \right)^t}$

With $t$ in years, substituting $t$ in the following table gives

time in months	time in years	calculations	Numerical value
1	$\frac{1}{{12}}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}$	19414.289
12	1	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}$	14000
14	$\frac{7}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	13192.012
38	$\frac{{19}}{6}$	$P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}$	6464.0859

Tags cloud

Rating

Views

Comments

\({a^n}{a^m} = {a^{n + m}}\)	\(\frac{{{a^n}}}{{{a^m}}} = {a^{n – m}}\)	\({\left( {{a^n}} \right)^m} = {a^{nm}} = {\left( {{a^m}} \right)^n}\)
\(\frac{1}{{{a^n}}} = {a^{ – n}}\)	\({a^n} = \frac{1}{{{a^{ – n}}}}\)	\({\left( {\frac{1}{a}} \right)^n} = \frac{1}{{{a^n}}}\)
\({\left( {ab} \right)^n} = {a^n}{b^n}\)	\({\left( {{a^{\frac{1}{n}}}} \right)^m} = {\left( {{a^m}} \right)^{\frac{1} {n}}} = {a^{\frac{m}{n}}}\)	\({a^0} = 1\) for each \(a \ne 0\)

Value of \(x\)
\(x < 0\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(1 < {a^x} < a\)
\(x = 1\)	\({a^x} = 1\)
\(x > 1\)	\(a < {a^x}\)

Value of \(x\)
\(x < 0\)	\({a^x} > 1\)
\(x = 0\)	\({a^0} = 1\)
\(0 < x < 1\)	\(0 < {a^x} < 1\)
\(x = 0\)	\({a^x} = 1\)
\(x > 1\)	\(0 < {a^x} < a < 1\)

Time	Time of years (\(s\))	Accumulated capital, in thousands, invest with continuous interest
Half-year	\(s = \frac{1}{2}\)	\(10{e^{0.0055\left( {\frac{1}{2}} \right)}} = 10.{\rm{\;}}027538\)
Two years	\(s = 2\)	\(10{\left( {1.00091667} \right)^{0.0055\left( 2 \right)}} = 10110.{\rm{\;}}607\)
38 months	\(s = \frac{{19}}{6}\)	\(10{\left( {1.00091667} \right)^{\frac{{19}}{6}}} = 10.\;175692\)

Year	elapsed time (\(t\))	Calculation	Population (Millions)
2021	0	\(P\left( t \right) = 126{\left( {1.0011} \right)^0}\)	126
2031	10	\(P\left( t \right) = 126{\left( {1.0011} \right)^{10}}\)	140.57
2051	30	\(P\left( t \right) = 126{\left( {1.0011} \right)^{30}}\)	174.95

Fixed term deposits	Annual rate	periods in a year	actual rate	Accumulated money in \(k\) months
two months	0.55%	6	\(\frac{{0.55\% }}{6} = 0.091667{\rm{\% }}\)	\(10000{\left( {1 + 0.00091667} \right)^{\frac{k}{2}}}\)
three months	1.87%	4	\(\frac{{1.87\% }}{4} = 0.4675{\rm{\% }}\)	\(10000{\left( {1 + 0.00461667} \right)^{\frac{k}{3}}}\)
six months	1.56%	2	\(\frac{{1.56\% }}{4} = 0.78{\rm{\% }}\)	\(10000{\left( {1 + 0.0078} \right)^{\frac{k}{6}}}\)

Time	Number of periods (\(k\))	Accumulated capital, in thousands, reinvested every two months
Half-year	3	\(10{\left( {1.00091667} \right)^3} = 10.{\rm{\;}}027525\)
Two years	12	\(10{\left( {1.00091667} \right)^{12}} = 10110.{\rm{\;}}557\)
38 months	19	\(10{\left( {1.00091667} \right)^{19}} = 10.\;175612\)

time in months	time in years	calculations	Numerical value
1	\(\frac{1}{{12}}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{1}{{12}}}}\)	19414.289
12	1	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^1}\)	14000
14	\(\frac{7}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	13192.012
38	\(\frac{{19}}{6}\)	\(P\left( t \right) = 20000{\rm{\;}}{\left( {1 – .30} \right)^{\frac{7}{6}}}\)	6464.0859